1. 기본 상황
2. 회귀 분석
3. 상관계수
4. 사분위수(IQR)를 사용하여 이상값 감지
5. Z-Score를 사용하여 이상값 감지
6. 상자 그림을 사용하여 이상값 감지
1. 기본 상황
대표값
= 데이터의 특성을 나타낼 수 있는 대표번호
4 기본통계
중심 경향: 데이터 분포가 중심에 얼마나 가까운지(중앙값, 최빈값, 평균)
확산: 데이터의 확산 및 집계 정도(분산, 표준편차, IQR)
Skewness: 분포의 비대칭 정도
첨도: 분포의 선명도
중심 경향을 나타내는 통계
1. 모드
정의: 가장 자주 발생하는 값
범주형 데이터에서는 주로 최빈값을 대표값으로 사용한다.
2. 중앙값
: 데이터를 크기순으로 정리했을 때의 중간값(=크기순으로 정리할 수 없는 데이터는 사용할 수 없습니다.)
: 서수 데이터의 대표값으로 적합한 통계량
: 이상값의 영향을 크게 받지 않습니다.
3. 산술 평균
: 데이터의 값을 모두 더한 후 데이터 개수로 나눈 값(=데이터는 더할 수 있는 값이어야 함)
: 연속 데이터에 주로 사용
: 이상값의 영향을 많이 받을 수 있습니다. (= 이상값을 필터링하고 평균을 찾을 수 있습니다.)
4. 가중 평균
: 데이터의 중요도에 따른 가중 평균 ex) 신뢰도가 높은 가중 데이터
5. 기하 평균
: 성장률 등 이전 시점의 평균 비율을 계산할 때 유용합니다.
: ex) CGAR(연평균성장률), 주가상승률
2. 회귀 분석
1. 필요성
: 다양한 변수를 고려하여 결과를 설명하고, 변수 간의 관계를 찾고, 반응 변수를 예측
2. 회귀분석의 정의
: 변수간의 모형을 구한 후 적합도를 측정하는 분석적 방법
예) 선형 회귀 모델
: 회귀 = 설명 변수 x와 응답 변수 y 사이에 함수 y = f(x) 적용
3. 회귀분석의 장점
: 둘 이상의 변수 사이의 관계보여주는 통계적 방법이다.
: 종속변수에 영향을 미침 각 독립 변수의 효과를 결정할 수 있습니다.하다.
4. 주의사항
: 상관관계는 인과관계를 설명하지 않습니다.
3. 상관계수
1. 피어슨 상관 계수
: 두 변수 간의 추세와 상관관계를 식별합니다.
: 절대값이 0.5~0.7 이상이면 상관관계가 강한 것으로 판단한다.
: -0.2 ~ 0.2는 약하거나 관련이 없는 것으로 해석됩니다.
4. IQR을 이용한 이상값 탐지
1. 정의
IQR = Q3-Q1 = 제3사분위수 – 제1사분위수
2. 이상치 검출 방법

: IQR을 기준으로 Q1-1.5*IQR ~ Q3+1.5*IQR에 해당하지 않는 기타 범위를 이상치로 판단한다.
즉, 이상값은 간격으로 판단됩니다.
3. _marking 이상값 사용 방법
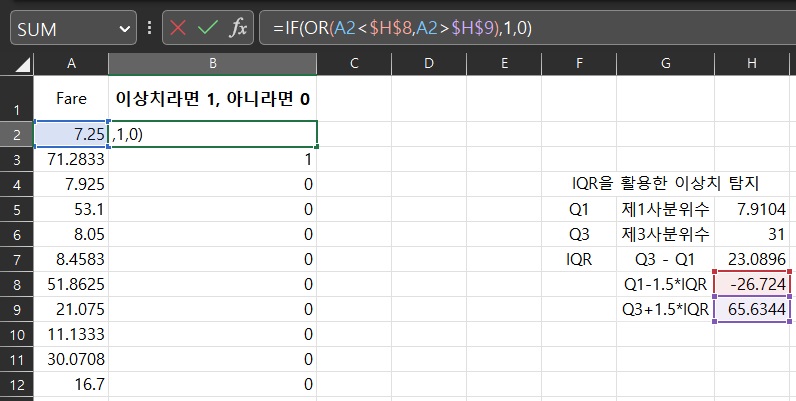
: 이와 같이 IF함수와 OR함수를 통해 데이터가 이상치인지 한눈에 구분할 수 있다.
: 이상값 탐지 방법으로 데이터가 정규분포가 아닌 한쪽으로 치우쳐 있을 때 주로 사용한다.
5. Z-Score(정규 분포)를 사용하여 이상값 감지
정규 분포는 평균과 표준 편차에 의해 결정됩니다.
: 먼저 데이터가 정규분포를 따르는지 확인하고 Z-Score 이상치 검출 방법을 사용해야 합니다.
: 보통 Z가 -3보다 작거나 3보다 크면 이상치로 판단한다.
6. 상자 그림을 사용하여 이상값 감지